After work I ran by chik-fil-a for dinner, because I definitely did not feel like trying to cook something. Chicken nuggets, waffles fries, and buffalo sauce... WHAT?! NO BUFFALO SAUCE? Chik-fil-a, I am disappoint.
Watched South Park and Tosh.O. Also gave the kitchen a good scrub down. You can probably put things on the counter without getting week-old crumbs with it now. And there aren't globs of peanut butter waiting to contaminate the bottom of your drink. How long will that last? Let's place some bets.
I'm starting to watch the Daily Show and Colbert Report more often. Also having trouble making myself go to sleep before midnight.
---
Lately, I've been getting more interested in half-pipes and skateboarding. Sure, it may just be because the X-games happened, and then the Dew Tour, and gravity games. I really remember enjoying skateboarding, and being more capable of doing physical activity. Trips to the skatepark were thoroughly enjoyed, but there are too few nearby.
So I started thinking about how fun it would be to build a half-pipe. Not only would that a fun project in itself, but a convenient way to get back into skateboarding. I looked at plans online. Most are fine, but if you really wanted to design a half-pipe, the amount of information is rather limited. I decided I could use some math skills and produce some equations that might help other people in their quest to design their own half-pipe.
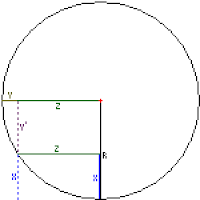
One of the first unknowns that popped up in my designing was how to determine lengths related to the the transition part of the ramp. For those of you who are new to the terminology, the "transition" is the part of the ramp that is curved upward. The transition follows the circumference of a circle. For mini-ramps, the radius of the circle is greater than the height of the ramp. For bigger ramps, or vert ramps, they use an entire quarter of a circle (and sometimes go straight up from there. These equations are not useful for large ramps.
I was able to ask for some assistance from Habs to churn through some of these equations. First, let's take a look at the drawing of what parts of the circle we want:
Now let's churn through some equations:
Another look at how this all fits together:
Hope this is helpful to somebody out there. And I hope I can continue to produce some useful information to the inner-workings of half pipe design in the future.



2 comments:
It should be noted that the division of work was as follows:
-Andy drew the pretty picture
-I came up with the equations
It should be noted that you cannot trust everything you read online.
I drew pictures, came up with the variables and given equations, and pushed the equations through the quadratic formula so that people have equations that are "plug and chug". (aka about half of whats on the math proof screen)
But yeah, Michael did help with the proof.
Post a Comment